"modeling" entries

Data modeling with multi-model databases
A case study for mixing different data models within the same data store.
Editor’s note: Full disclosure — the author is a developer and software architect at ArangoDB GmbH, which leads the development of the open source multi-model database ArangoDB.
In recent years, the idea of “polyglot persistence” has emerged and become popular — for example, see Martin Fowler’s excellent blog post. Fowler’s basic idea can be interpreted that it is beneficial to use a variety of appropriate data models for different parts of the persistence layer of larger software architectures. According to this, one would, for example, use a relational database to persist structured, tabular data; a document store for unstructured, object-like data; a key/value store for a hash table; and a graph database for highly linked referential data. Traditionally, this means that one has to use multiple databases in the same project, which leads to some operational friction (more complicated deployment, more frequent upgrades) as well as data consistency and duplication issues.
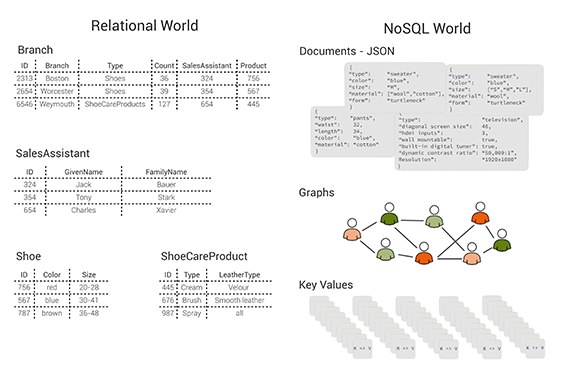
Figure 1: tables, documents, graphs and key/value pairs: different data models. Image courtesy of Max Neunhöffer.
This is the calamity that a multi-model database addresses. You can solve this problem by using a multi-model database that consists of a document store (JSON documents), a key/value store, and a graph database, all in one database engine and with a unifying query language and API that cover all three data models and even allow for mixing them in a single query. Without getting into too much technical detail, these three data models are specially chosen because an architecture like this can successfully compete with more specialised solutions on their own turf, both with respect to query performance and memory usage. The column-oriented data model has, for example, been left out intentionally. Nevertheless, this combination allows you — to a certain extent — to follow the polyglot persistence approach without the need for multiple data stores. Read more…

Graphs in the world: Modeling systems as networks
See, extract, and create value with networks.
Networks of all kinds drive the modern world. You can build a network from nearly any kind of data set, which is probably why network structures characterize some aspects of most phenomenon. And yet, many people can’t see the networks underlying different systems. In this post, we’re going to survey a series of networks that model different systems in order to understand different ways networks help us understand the world around us.
We’ll explore how to see, extract, and create value with networks. We’ll look at four examples where I used networks to model different phenomenon, starting with startup ecosystems and ending in network-driven marketing.
Networks and markets
Commerce is one person or company selling to another, which is inherently a network phenomenon. Analyzing networks in markets can help us understand how market economies operate.
Strength of weak ties
Mark Granovetter famously researched job hunting and discovered the Strength of Weak Ties. Read more…

The tensor renaissance in data science
The O'Reilly Data Show Podcast: Anima Anandkumar on tensor decomposition techniques for machine learning.
After sitting in on UC Irvine Professor Anima Anandkumar’s Strata + Hadoop World 2015 in San Jose presentation, I wrote a post urging the data community to build tensor decomposition libraries for data science. The feedback I’ve gotten from readers has been extremely positive. During the latest episode of the O’Reilly Data Show Podcast, I sat down with Anandkumar to talk about tensor decomposition, machine learning, and the data science program at UC Irvine.
Modeling higher-order relationships
The natural question is: why use tensors when (large) matrices can already be challenging to work with? Proponents are quick to point out that tensors can model more complex relationships. Anandkumar explains:
Tensors are higher order generalizations of matrices. While matrices are two-dimensional arrays consisting of rows and columns, tensors are now multi-dimensional arrays. … For instance, you can picture tensors as a three-dimensional cube. In fact, I have here on my desk a Rubik’s Cube, and sometimes I use it to get a better understanding when I think about tensors. … One of the biggest use of tensors is for representing higher order relationships. … If you want to only represent pair-wise relationships, say co-occurrence of every pair of words in a set of documents, then a matrix suffices. On the other hand, if you want to learn the probability of a range of triplets of words, then we need a tensor to record such relationships. These kinds of higher order relationships are not only important for text, but also, say, for social network analysis. You want to learn not only about who is immediate friends with whom, but, say, who is friends of friends of friends of someone, and so on. Tensors, as a whole, can represent much richer data structures than matrices.

