Let’s examine the followers of some popular Twitter users by asking the (Freakonomics-inspired) question, What do Tim O’Reilly, Lady Gaga, and Marissa Mayer all have in common? Although it may initially seem like an obnoxious question to ask, some of the answers may intrigue you once you begin to take a closer look at the data. (Although dashingly good looks might be one thing that they all have in common, we’ll let the data do the talking and stick with Twitter followers as the basis of computing similarity.)

Which two of these three accomplished entrepreneurs are most alike? It all depends on the features that you’re comparing!
Goals
The initial idea behind this entire series on Twitter influence is that it would be an interesting and educational experiment in data science to put Tim O’Reilly‘s ~1.7 million followers under the microscope and explore the correlation between popularity (based upon number of followers) and Twitter influence.
In order to draw some meaningful comparisons, however, we’ll need to consider at least one other account. Marissa Mayer seems like a fine selection for comparison since her Twitter account is similar yet different to Tim’s account. For example, she’s also a “tech celebrity” and business executive. However, her particular expertise is not quite the same, and she only has about one-fourth as many followers. (Or so it would initially appear…)
Just to make this interesting, let’s further mix things up a bit by introducing a wildcard. Lady Gaga seems as good a choice as any to introduce a bit of unexpected fun into the situation. She is one of the ten most popular Twitter users based upon number of followers, an accomplished entrepreneur, and surely draws interest from a broad cross-section of the population. The introduction of a third account also provides the opportunity to draw some additional comparisons, so let’s compute the Jaccard index for the various combinations of these three accounts and see what turns up. The Jaccard index measures similarity between sample sets, and is defined as the size of the intersection divided by the size of the union of the sample sets, or, more plainly, the amount of overlap between the sets divided by the total size of the combined set. This is a simple way to measure and compare the overlap in followers.
Results
The full results (example code, notes, and the results from executing each cell) are available as an IPython Notebook, and you are encouraged to review it in depth. For convenience, a summary of the key results that you’ll see computed in the notebook follow:
- Approximately 50% of Tim O’Reilly’s ~1.7 million followers are “suspect” in the sense that they may be inactive accounts or spam bots. In comparison, only about 15% of Marissa Mayer’s ~460k followers are suspect according to the same criteria.
- Although mostly speculative, this difference might be explainable by a massive wave of spam-bots targeting popular users back in 2009 when Twitter experienced some unprecedented growth in its number of users. (For example, a closer look at the data reveals that ~66% of Tim O’Reilly’s followers joined Twitter in 2009.)
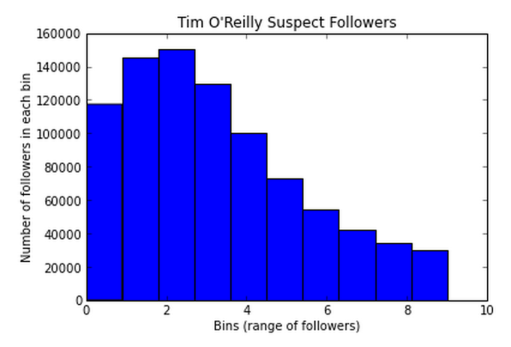
A histogram of Tim O’Reilly’s followers who have fewer than 10 followers of their own. Approximately 50% of these followers are “suspect” in that they may be spam-bots or inactive accounts; decreasing the threshold to 5 decreases the number to just under 40%.
- Approximately 25% of Tim O’Reilly’s (“non-suspect”) followers also follow Lady Gaga as compared to only about 18% for Marissa Mayer.
- In other words, there appears to be a slightly stronger affinity between Tim O’Reilly and Lady Gaga than between Marissa Mayer and Lady Gaga.
- Lady Gaga has a higher Jaccard similarity to Tim O’Reilly than to Marissa Mayer. (However, Tim O’Reilly and Marissa Mayer have a much higher Jaccard similarity to one another than either one of them have to Lady Gaga, as might have been reasonably expected from their strong technology backgrounds.)
- Tim O’Reilly and Marissa Mayer have ~100k followers in common, and even once this number is adjusted for suspect followers, there are still ~95k followers in common. This is a high number but doesn’t seem all that surprising.
- What may seem a bit unexpected is that once you introduce Lady Gaga, this number only drops to ~25k. In other words, the total number of followers that Tim O’Reilly, Marissa Mayer, and Lady Gaga all have in common amongst the three of them is still about 25k accounts.
Perhaps the broad takeaway that addresses our initial inquiry about using popularity as an indicator of clout is that “number of followers” is not as clear cut a heuristic as it may have first seemed. After all, the actual gap between Tim O’Reilly and Marissa Mayer appears to be considerably smaller than it once appeared after making a simple adjustment for so-called “suspect” followers.
But what do Tim O’Reilly, Lady Gaga, and Marissa Mayer have in common? At least one way of answering the question is that there appears to be that there at least 25k common fans who are interested in all three of them. After all, Twitter is an interest graph. A closer analysis of these common account profiles could prove quite interesting and is a recommended exercise.
Although nothing definitive was proven, it seems quite likely that a coarse filter on an account’s followers is a good starting point. It wouldn’t be too difficult to perform some additional filtering to increase the precision of identifying abandoned accounts or spam bots that cannot be influenced in order to more accurately narrow in on a base metric for computing Twitter influence. You now have the tools and a good starting point to do just that — and a lot of other fun stuff.
By the way, you notice that we didn’t tell you how many of Lady Gaga’s followers appear to be spambots or inactive. That is the topic for another post to follow. (Unless, of course, you beat me to the punch!)
Enjoy!
Resources
- An HTML export of the IPython Notebook for this post
- The collection of IPython Notebooks containing the source notebook for this post
- Mining the Social Web on GitHub
- Screencasts that show you how to install the social web mining toolkit as a virtual machine
- Previous posts in this series on Twitter influence
This originally appeared on miningthesocialweb.com and has been lightly edited for brevity.
